数学图论中的一笔画问题与抖音神题5×5点阵缺一点时的连线问题
先说题目,数学图论中的一笔画问题。“一笔画”从字面理解就是一笔画出,它是现在研究线段的数目和它们之间的连接关系有关代表。如果不好理解举个例子:汉字“日”和“中”字都可一笔画,而“田”和“目”则不能。连通的图形可以画出,非连通有空余的不能画出如“回、国”。
再说题目的第二部分“抖音神题5×5点阵缺一点时的连线问题”,这是在抖音或其他短视频平台非常火的题目,题目是这个样子的,题目未写全其实还有不能斜连、跳连的要求。
这种题与上面说的一笔画有什么联系?我个人看着是没有什么联系,但说不定有看到的朋友能找到联系。
好,现在重新探讨这两种题:
一笔画问题:
如下图中:“日、中、口、几、己”均可以一笔画出,笔不离纸,而“品、回、吕”中间有未连通部分,所以不能一笔画出,而“田、目”虽然连通,但却不能一笔画出,为研究为何如“目、田”不能一笔画出的原因,我们引入部分概念。

第一、能一笔画的图,必须是连通的,没有连成一体的图不能一笔画出。
第二、我们把和1条、3条、5条等奇数条线相连的点叫做奇点,把和2条、4条、6条等偶数条相连的点叫做偶点。
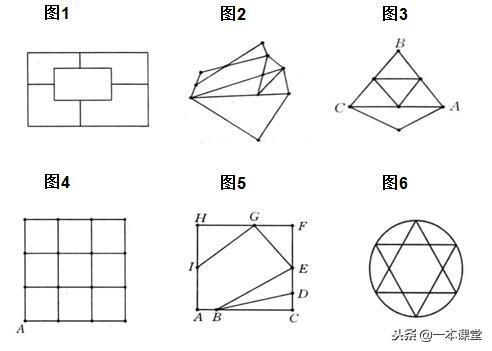
如“田、目”中,田有均4个奇点,其中田有5个偶点、目有四个偶点。不止是汉字,图形中也是如此。比如下图A图有2个奇点、2个偶点但可以一笔画出,图B有4个奇点、1个偶点,但不能一笔画出,图C有2个奇点、5个偶点可以一笔画出。
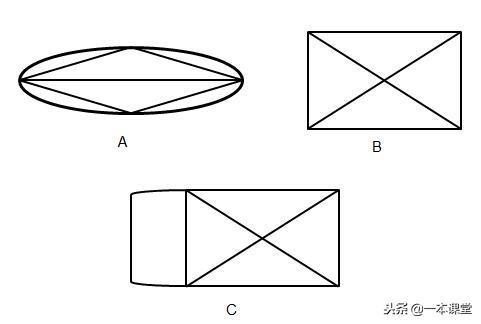
只将A图的画法举例,从左至右,其实也是从一个奇点出发最后到另一个奇点结束:
对于这种一笔画问题,欧拉总结出了相关定理,即欧拉定理:
第一、凡是由偶点组成的连通图,一定可以一笔画成,画时可以从任一偶点出发,并以该偶点结束。
第二、凡是只有2个奇点组成的连通图,一定可以一笔画出,画时必须从其中一个奇点为起点,另一个奇点为终点。
第三、其他情况不能一笔画出。
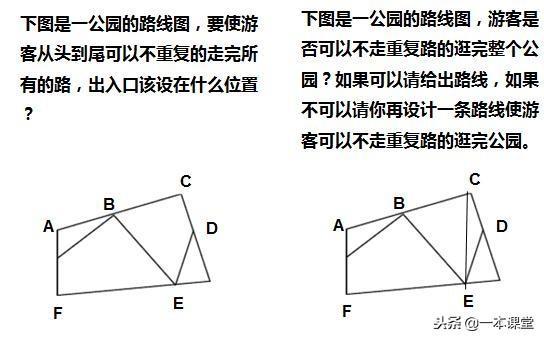
下图中是否有可以一笔画出的图,不妨指出,在小学中会以出入口的形式考题:
比如下面两题:
另外还有多笔画和多笔画转一笔画,这里不再说以后再谈。
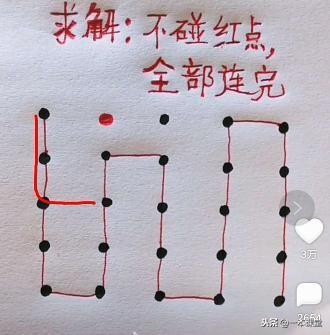
下面谈一谈上面给出的抖音神题。换种形式,这里我要说一下,回答是:“不能!”,这虽然不是考试试题,一般考试试题可能回答能,然后给出解题思路,但这里说不能也需要给出解题思路。
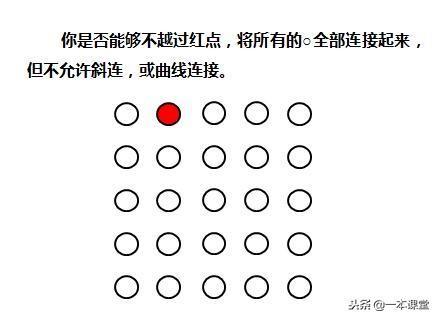
为什么不能呢,我们看到一个点它只能向上、下、左、右相邻的位置走,那么我们将所有的点进行编码,虽然点的位置不同,但三个点中,不相邻的点没有必然关系,我们可以仅用1、0进行编号,如图所示画笔走向一定是1→0→1→0或0→1→0→1,也就是1的数量一定要等于0或多1个又或是少1个,而下图中1有13个,而0只有11一个,1比0多出2个,所以一定无法画出。

那么如果将红点更改位置比如下面四幅图,则可以先判断哪个可以不过红点一笔连接起来,哪个不可以。
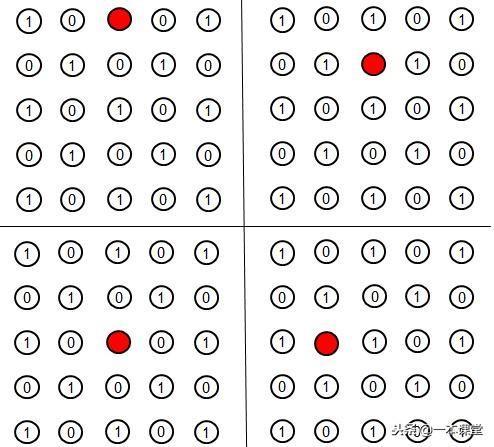
有没有试出来?其实对于上面图形来说如果编码为1的改成红点便可以连接起来,但编码为0的点改为红点便不可以(初始有13个1,12个0)。这是5×5点阵,如果是6×6的会是如何?我们随意选了一点改为红色,连接图如下(其他改变方式可以自行试验):
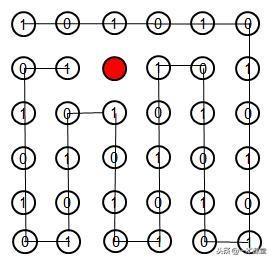
现在是1个点为红色,下面试一下改2点,下面左图已经做出,也请人试一试右侧的图是否可以连成?我连了连没有成功。
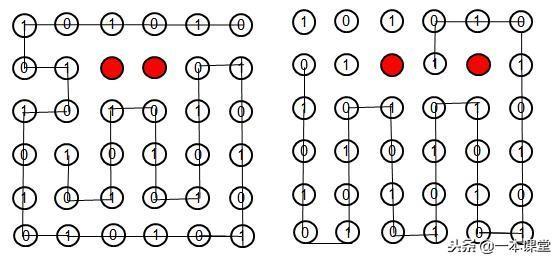
最后想问对于这种图形是否也满足编码为1的点数与编码为0的点数对比相等或多一个,少一个就能连接起来呢 ?
原创不易,喜欢请点关注,如有错误也请指出,谢谢。